Last week I returned from the Dynamic Walking 2017 conference, where I had a poster and five minute talk on some of the numerical trajectory optimization work I’ve been doing for spring loaded inverted pendulums. More specifically, I was trying to determine what kinds of strategies the optimizer discovers when recovering from landing unexpectedly on an ice patch. This post will give a quick overview of the results but for more details please see my abstract submission and optimizer setup description.
To start off with, I varied the width of the ice patch as well as the initial state of the SLIP on the patch. The end state constraint was that the SLIP had to finish in a vertical stance (hip over toe) to the right of the patch, so as to hypothetically be able to continue walking. For each scenario, the optimizer ran through a two-stance-phase solution (step directly from the ice patch to the goal) and a three-stance-phase solution (first step backwards, then launch across the patch to the goal), trying to minimize the mechanical work exerted by the torque and leg extension actuators. Over hundreds of randomly initialized trials, the optimizer generally converged to the following five “key” strategies:
Takeaways
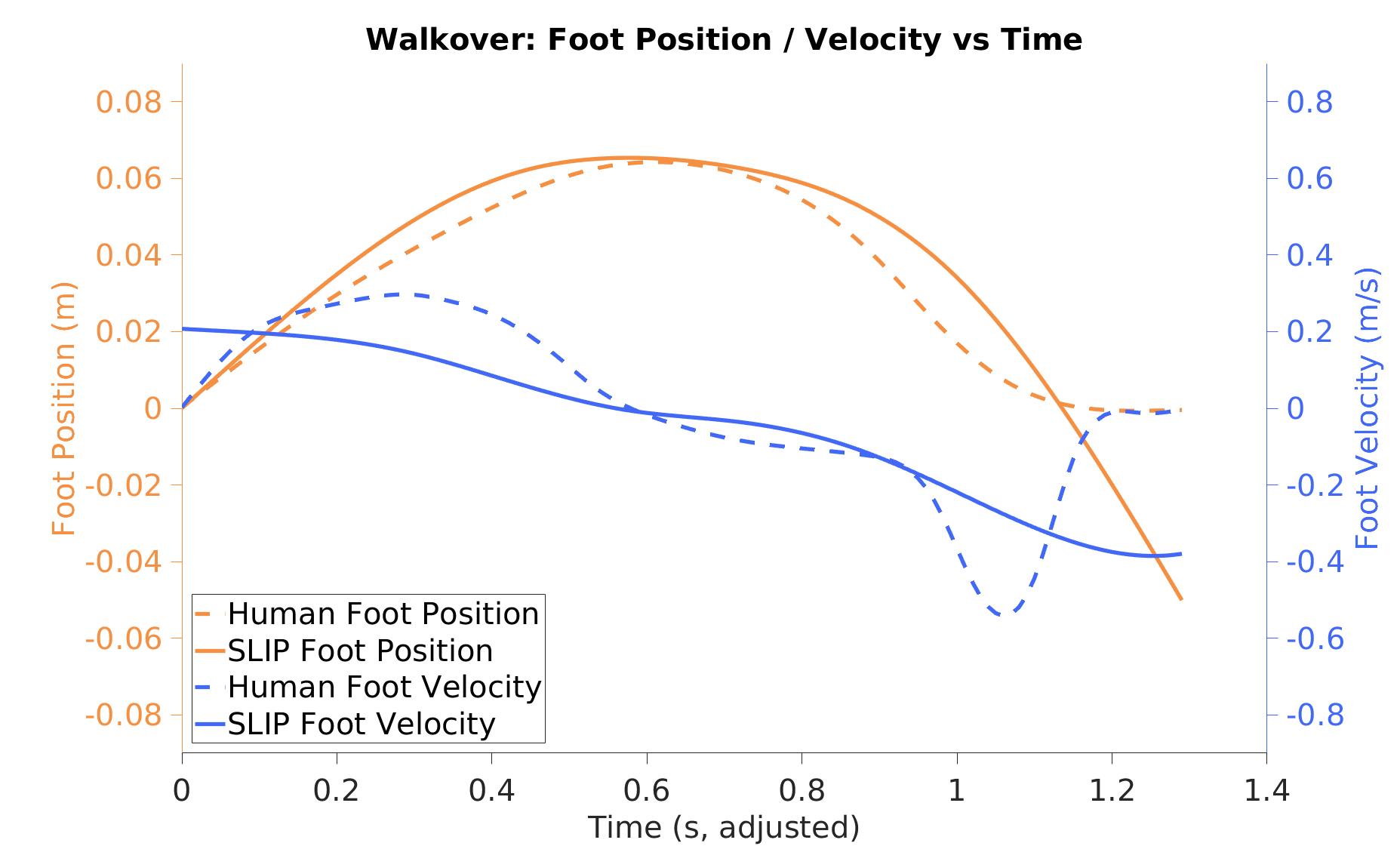
One interesting observation is that the solution strategies can be primarily categorized by the movement of the foot during the sliding phase. In addition, previous studies of human SLIP recovery revealed the same walk-over and skate-over strategies discovered by the optimizer [1]. These similarities suggests that on some level humans might be prioritizing energy efficiency when recovering from slipping. I then more closely compared the human foot dynamics data with the optimizer’s. Here are the sliding phase comparison graphs using data from [1] and the simulations:
As you can see, the general arc of the foot position is matched by the optimizer but some of the nuances of the foot velocity profile are lost. Most notably, in the walkover case humans regulate their sliding foot velocity to zero by the end of the stance phase but my optimizer did not. These differences might be attributable to some of the errors listed below.
Errors
This work is certainly not perfect and there are a some flaws that may have adversly impacted the results. These include:
- Disregarding the double support phase during SLIP recovery
- Disregarding leg swing cost during flight phase
- Not modelling static friction
- Possible local optima in the simulation
Robotics Applications
I’d like to end with a quick note about how these kinds of optimization exercises can be used to not only improve our understanding of human locomotion but also develop practical robot controllers. If we assume that the robot has some knowledge of its state and an upcoming obstacle, it could be feasible to use that information to select an appropriate traversal strategy from a library of previously-computed solutions. That rough version of the trajectory could then be used to initialize an on-board trajectory optimizer or some other method that ultimately controls the actuators.
Sources
[1] T. Bhatt, J. D. Wening, and Y. C. Pai, “Adaptive control of gait stability in reducing slip-related backward loss of balance,” Experimental Brain Research, vol. 170, no. 1, pp. 61–73, 2006.

Leave a Reply