Tutorial: Direct Collocation Trajectory Optimization with Matlab

In the previous tutorial, we focused on single shooting trajectory optimization, which involved time-discretizing the control input and simply integrating the dynamics. The desired end state was then added as a constraint to fmincon. Here, we focus on a different trajectory optimization technique, known as direct collocation.

Simultaneous Optimization

The core difference between shooting methods and simultaneous methods such as direct collocation is that in simultaneous methods the states are discretized along with the control inputs. These state variables are added to the vector of function parameters, and constraints are added at every discretization point to ensure that the dynamics are evolving correctly. The state vector effectively becomes the following:

$x = \begin{bmatrix}y_1 \\ u_1 \\ y_2 \\ u_2 \\ ... \\ y_n \\ u_n \end{bmatrix}$

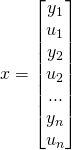
(Optionally, the time of the simulation can also be included in the state as a variable for the optimizer). Each constraint would be formulated as follows:

$y_i = y_{i-1} + \frac{\dot{y}_i + \dot{y}_{i-1}}{2}\cdot dt$

Where $\dot{y}_i$ would depend on $u_i$ . Note that in this formulation the state derivative is linearly interpolated between the two grid points, known as trapezoidal quadrature. Other schemes, such as Hermite-Simpson collocation, are slightly more complex.

Since fmincon’s equality constraints are given as a vector of values to drive to zero, the end equality constraints would look something like:

$ceq = \begin{bmatrix} y_{desired initial} - y_1 \\ y_2 - (y_{1} + \frac{\dot{y}_{2} + \dot{y}_{1}}{2} \cdot dt) \\ y_{3} - (y_{2} + \frac{\dot{y}_3 + \dot{y}_{2}}{2}\cdot dt) \\ ... \\ y_{end} - (y_{end-1} + \frac{\dot{y}_{end} + \dot{y}_{end-1}}{2}\cdot dt) \\ y_{desired end} - y_{end} \end{bmatrix}$

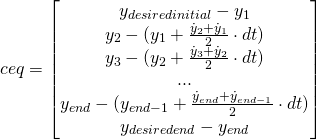
Let’s look at an example, using the same double integrator plant from the previous tutorial.

double_integrator.m

global gridN
gridN = 20;

tic
% Minimize the simulation time
time_min = @(x) x(1);
% The initial parameter guess; 1 second, gridN positions, gridN velocities,
% gridN accelerations
x0 = [1; linspace(0,1,gridN)'; linspace(0,1,gridN)'; ones(gridN, 1) * 5];
% No linear inequality or equality constraints
A = [];
b = [];
Aeq = [];
Beq = [];
% Lower bound the simulation time at zero seconds, and bound the
% accelerations between -10 and 30
lb = [0;    ones(gridN * 2, 1) * -Inf;  ones(gridN, 1) * -10];
ub = [Inf;  ones(gridN * 2, 1) * Inf;   ones(gridN, 1) * 30];
% Options for fmincon
options = optimoptions(@fmincon, 'TolFun', 0.00000001, 'MaxIter', 10000, ...
                       'MaxFunEvals', 100000, 'Display', 'iter', ...
                       'DiffMinChange', 0.001, 'Algorithm', 'sqp');
% Solve for the best simulation time + control input
optimal = fmincon(time_min, x0, A, b, Aeq, Beq, lb, ub, ...
              @double_integrator_constraints, options);

% Discretize the times
sim_time = optimal(1);
delta_time = sim_time / gridN;
times = 0 : delta_time : sim_time - delta_time;
% Get the state + accelerations (control inputs) out of the vector
positions = optimal(2             : 1 + gridN);
vels      = optimal(2 + gridN     : 1 + gridN * 2);
accs      = optimal(2 + gridN * 2 : end);

% Make the plots
figure();
plot(times, accs);
title('Control Input (Acceleration) vs Time');
xlabel('Time (s)');
ylabel('Acceleration (m/s^2)');
figure();
plot(times, vels);
title('Velocity vs Time');
xlabel('Time (s)');
ylabel('Velocity (m/s)');
figure();
plot(times, positions);
title('Position vs Time');
xlabel('Time (s)');
ylabel('Position (m)');

disp(sprintf('Finished in %f seconds', toc));

double_integrator_constraints.m

function [ c, ceq ] = double_integrator_constraints( x )
    global gridN
    % No nonlinear inequality constraint needed
    c = [];
    % Calculate the timestep
    sim_time = x(1);
    delta_time = sim_time / gridN;
    % Get the states / inputs out of the vector
    positions = x(2             : 1 + gridN);
    vels      = x(2 + gridN     : 1 + gridN * 2);
    accs      = x(2 + gridN * 2 : end);
    
    % Constrain initial position and velocity to be zero
    ceq = [positions(1); vels(1)];
    for i = 1 : length(positions) - 1
        % The state at the beginning of the time interval
        x_i = [positions(i); vels(i)];
        % What the state should be at the start of the next time interval
        x_n = [positions(i+1); vels(i+1)];
        % The time derivative of the state at the beginning of the time
        % interval
        xdot_i = [vels(i); accs(i)];
        % The time derivative of the state at the end of the time interval
        xdot_n = [vels(i+1); accs(i+1)];
        
        % The end state of the time interval calculated using quadrature
        xend = x_i + delta_time * (xdot_i + xdot_n) / 2;
        % Constrain the end state of the current time interval to be
        % equal to the starting state of the next time interval
        ceq = [ceq ; x_n - xend];
    end
    % Constrain end position to 1 and end velocity to 0
    ceq = [ceq ; positions(end) - 1; vels(end)];
end

If you run this code, you should see that the optimizer converges to the same bang-bang control it did with single shooting.

Why Direct Collocation?

Now that you’ve read through the above code and hopefully better understand direct collocation, you may be wondering the advantages and disadvantages are of simultaneous methods over shooting methods. Christian Hubicki succinctly summarizes the difference in his dissertation on optimization for robotics (36-38) [1]:

There is a notable computational advantage to this somewhat non-intuitive formulation. With direct collocation, the relationship between variables and constraints can be expressed entirely with closed-form equations, even if the integral of our dynamical equations cannot (which is frequently the case in legged locomotion). This means that both the values of the objective, constraints, and the gradients with respect to all optimization variables can also be represented in closed form, greatly accelerating the computation time of the optimization. In practice, this computational efficiency and smoothness of the resulting equations has allowed our implementations to solve direct collocation problems with over 10,000 variables and constraints.

One apparent downside of direct collocation is a loss of dynamical accuracy. [Shooting methods] are still free to use variable-time-step time-marching integrators to integrate the dynamics as accurately as possible, but direct collocation often operates with far fewer integration steps and are roughly fixed in size. However, the degree to which direct collocation makes optimization faster often allows for the user to select quite fine resolutions, e.g. hundreds of time points. Further, in this application, the results of these optimizations will often be regulated by a locally stabilizing controllers anyhow, making a small degree of dynamical inaccuracy akin to noise in the system.

As an aside, other sources such as Matthew Kelly’s write-up caution against using variable time step integrators for shooting methods [2].

Sources

https://ir.library.oregonstate.edu/xmlui/handle/1957/54820?show=full
http://www.matthewpeterkelly.com/research/MattKelly__Transcription_Methods_for_Trajectory_Optimization.pdf

Posted

August 29, 2016

robotics, simulations, trajectory optimization

Samuel Pfrommer

Tags:

direct collocation, fmincon, function optimization, matlab, trajectory optimization

Comments

4 responses to “Tutorial: Direct Collocation Trajectory Optimization with Matlab”

Deepa

March 21, 2020

Hello Samuel,
I’m following the description given here to solve an optimal control problem of the form defined https://scicomp.stackexchange.com/questions/34672/automatically-generate-constraints-for-trajectory-optimization?noredirect=1&lq=1

I’m not sure how the equality constraints have to be defined. For example,

in the code provided above

function [ c, ceq ] = double_integrator_constraints( x )

Could you please explain how the input argument, x, is computed?
Also, please explain what is ydesiredend mentioned in equality constraints?

In my problem, only the initial conditions are defined for the dynamical constraints and the terminal conditions are not available. In that case , I am not sure how the constraints have to be defined.

Reply
1. Samuel Pfrommer
  
  March 26, 2020
  
  Hello,
  
  fmincon is an iterative method which passes its current guess for x as an argument to the constraint function; it then performs gradient estimation to drive the output of the constraint function to zero. y_{desiredend} is the desired final position for the particle, which we equality constrain to the final position of the trajectory guess.
  
  It seems like trajectory optimization might not be the best fit for your problem–it’s generally used more for optimizing a time-varying control signal subject to dynamical constraints. I’d look more into system identification methods for differential equations.
  
  Reply
Harley Towler

December 14, 2021

Hi Samuel,

I was wondering if you could help with the following problem.

I have a starting and ending location within 3D space, and I am interested in finding the initial velocity conditions, when I know the time of flight and how the object decelerates due to drag. How would I solve this problem quickly?

Currently, I am iterating through various x, y and z velocities (within certain bounds) from which the simulated ending location error is minimal.

Thanks

Reply
1. Samuel Pfrommer
  
  January 10, 2022
  
  Hi Harley,
  
  Consider first whether the problem can be reduced to the planar case — namely, the vertical plane between the starting and ending locations. Then you can just consider horizontal and vertical initial velocities in the plane and use trig functions to get the x and y velocities for the original problem.
  
  Now for the planar case, I assume you’re considering Newton drag (drag proportional to velocity squared). There is no convenient closed-form solution for the dynamics here, but it can be solved numerically. The simplest approach would be to modify the flight_constraint function in the single shooting optimization tutorial to perform a numerical integration of the dynamics. This can be accomplished by integrating the differential equation from the Wikipedia article with one of matlab’s ODE solvers. Generally it’s not recommended to solve an ode / numerical problem within a larger optimization since finite solver precision can make the outer gradients noisy. The more disciplined approach would be to add the drag dynamics to each direct collocation time step. But for your problem the single shooting approach should work fine.
  
  Reply