Previously, I’ve written short introductions to numerical trajectory optimization here and here—if you’re unfamiliar with the basics, I recommend you check those out first.
This write up expands upon a section of my research paper (which I hope to finish soon) and is meant to be a walkthrough of how to apply numerical trajectory optimization to real-world scenarios.
The Problem
The Spring Loaded Inverted Pendulum (SLIP) model is often used to approximate human running dynamics. Fundamentally, SLIP hoppers represent the mass of the torso as a point at the hip and connect the hip to the foot via a spring. In other words, the biped becomes a pogo stick, bouncing from foot to foot with each step.
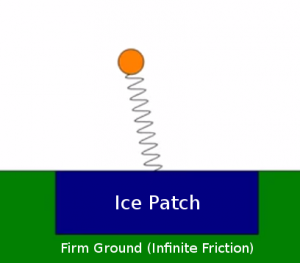
We consider the case where a running planar biped steps on an unforeseen ice patch, surrounded with high-friction ground on each side. The question then becomes this: should the robot attempt to use its momentum to traverse the patch in one step, or first step backwards and then launch itself over the patch to the other side?
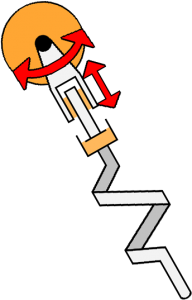
Modified SLIP
In addition to the basic SLIP model, I included a few modifications:
- Damper in series with spring
- Hip torque actuation
- Second derivative of neutral length actuation
- Foot mass (for sliding)
SLIP Dynamics
Before constructing the optimization problem, we need to know the dynamics of the system. A “phase” represents a section of a trajectory with continuous state and one set of governing equations. Three different types of phases are possible in this system: standing on ground, slipping on ice, and flying through the air. Since the first two cases are similar, we will first handle them together and then discuss flight phases.
Stance Phase
Let (![]() ,
,![]() ) be the hip position,
) be the hip position, ![]() be the toe horizontal position,
be the toe horizontal position, ![]() be the spring coefficient,
be the spring coefficient, ![]() be the damping coefficient,
be the damping coefficient, ![]() be the SLIP length,
be the SLIP length, ![]() be the actuated SLIP length (or neutral spring length),
be the actuated SLIP length (or neutral spring length), ![]() be the hip torque,
be the hip torque, ![]() and
and ![]() be the hip and toe masses, respectively, and
be the hip and toe masses, respectively, and ![]() be the gravitational constant. The state of the SLIP can be then represented as follows:
be the gravitational constant. The state of the SLIP can be then represented as follows:
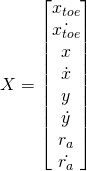
And the SLIP length ![]() can then be written as:
can then be written as:
(1) ![]()
Differentiating by the chain rule, we get the following equation for the time derivative of ![]() :
:
(2) ![]()
The force exerted by the spring-damper combination can then be expressed as follows:
(3) ![]()
While the force exerted by the hip torque on the ground is simply:
(4) ![]()
Realizing that the cosine of the angle between the SLIP and the ground is equal to ![]() and the sine is equal to
and the sine is equal to ![]() , it is possible to express the acceleration of the hip:
, it is possible to express the acceleration of the hip:
(5) ![]()
(6) ![]()
However, it is also necessary to know the acceleration of the toe on the ice. We first determine the ground reaction force as follows:
(7) ![]()
The force of friction on the toe is then given as:
(8) ![]()
Where the ![]() serves as a smooth approximation of a sign function, whose discontinuities create convergence difficulties for the optimizer.
serves as a smooth approximation of a sign function, whose discontinuities create convergence difficulties for the optimizer.
Finally, the acceleration of the toe can be expressed as follows:
(9) 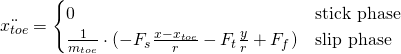
This concludes the SLIP dynamics during both slippery and high-friction stance phases.
Flight Phase
Flight phases are governed by the standard equations for ballistic trajectories and are triggered when the ground reaction force intersects zero. First, we declare a free variable, ![]() . The following equations then result:
. The following equations then result:
![]()
![]()
Where all “to” subscripts represent takeoff states and all “land” subscripts represent landing states.
Formulating constraints
Within a certain phase, constraints are formulated using direct collocation, which discretizes the states and control inputs at evenly-spaced nodes and enforces the dynamics between nodes using hard equality constraints. The following inequality constraints are also enforced at every node:

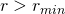
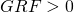
- The ground reaction force must be positive within a phase for ground contact to occur. The only exceptions are the last nodes of stance phases that have a flight phase following them (instead are equality constrained to zero). The last node of the last phase, however, does need the GRF inequality constraint.
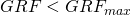
- Prevents unreasonably large GRF forces that might damage the robot.
There also need to be constraints governing phase transitions. Since the flight dynamics are solvable in closed form, this ultimately amounts to linking the end of one stance phase to the beginning of the next in a way which obeys the flight dynamics. Discretizing the state along the flight path is unnecessary.
As mentioned previously, the flight time parameter ![]() here is really critical. I first fooled around with a bunch of different strategies (for example parameterizing a completely separate landing state, with the landing angle and length inferred from the first node of the next phase, and then equality constraining the two). None converged reliably; many thanks to Christian Hubicki for pointing me in the right direction here.
here is really critical. I first fooled around with a bunch of different strategies (for example parameterizing a completely separate landing state, with the landing angle and length inferred from the first node of the next phase, and then equality constraining the two). None converged reliably; many thanks to Christian Hubicki for pointing me in the right direction here.
The best method turned out to be evaluating the end state of the ballistic flight trajectory from the take off state and flight time, and then equality constraining that with the first node of the next stance phase. The specific variables that were constrained from the flight phase were ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . The ground reaction force at takeoff and
. The ground reaction force at takeoff and ![]() at touchdown are constrained to zero, and
at touchdown are constrained to zero, and ![]() is constrained equal to
is constrained equal to ![]() at touchdown.
at touchdown.
There are a few more variables and constraints that are important to note. Each stance and flight phase had a time parameter, which was bounded using the lower bound and upper bound arguments to fmincon. Similarly, the max/min actuated leg length second derivative and hip torque were also bounded in the fmincon bounds arguments. The toe x position was bounded to be within the ice patch for the slippery phase and outside for the sticky phase. The initial SLIP state was constrained to a starting position over the ice patch, and the final SLIP x and toe x were constrained to be slightly to the right of the ice patch.
Objective functions
Cold-initializing an energy-optimizing objective with random parameters often results in failure to converge due to the large number of parameters and constraints. Therefore, a three-step optimization was used:
- Constant objective function (find any trajectory which satisfies constraints)
- Resulting trajectory is fed into impulse cost function:
(10)
![Rendered by QuickLaTeX.com \begin{equation*} C_{imp} = \sum_{n=1}^{N_{phase}} \sum_{i=1}^{N_{grid}} [(\ddot{r_a}_{n,i} \cdot \Delta t_n)^2 + (\tau_{n,i} \cdot \Delta t_n)^2] \end{equation*}](https://sam.pfrommer.us/wp-content/ql-cache/quicklatex.com-fbadbe0f816e68015d4ea2dd85f626f3_l3.png)
Where
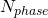 is the number of stance phases,
is the number of stance phases, 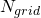 is the number of discretization nodes per stance phase, and
is the number of discretization nodes per stance phase, and 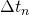 is equal to the nth stance phase time
is equal to the nth stance phase time 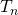 divided by
divided by 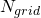 .
. - Output trajectory of impulse cost function is fed into work cost function:
(11)
![Rendered by QuickLaTeX.com \begin{equation*} \sum_{n=1}^{N_{phase}} \bigg[\int_{0}^{T_n} |F_s \cdot \dot{r_a}|dt + \int_{\theta_{td}}^{\theta_{to}}|\tau d\theta|\bigg] \end{equation*}](https://sam.pfrommer.us/wp-content/ql-cache/quicklatex.com-b74b9dbef71e3e1d2fd5ddf1c2a6a2aa_l3.png)
Since the absolute value function is inherently nonsmooth—creating optimizer convergence problems—a smooth approximation was employed:
(12)
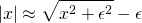
Where
 is about
is about 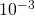 .
.
Problem Formulation
As mentioned previously, the trajectory optimization problem was transcribed using direct collocation with 10 nodes per stance phase. For linking one node to the next within a stance phase, dynamics were integrated using trapezoidal quadrature. Matlab’s fmincon was used for the optimization, with the SQP algorithm specified. Jacobians were symbolically calculated to accelerate convergence. The whole three-step optimization takes on the order of a few minutes to complete and converges reliably from random initial parameters.
Code
main.m
GEN_CONSTRAINTS = true;
GEN_COSTS = true;
sp = SimParams(['str'], [0,1], [1.1; 0; 1.1-cosd(45); 0; ...
sind(45); 0; 1; 0], 1.1);
% Options for optimizing the constant cost function
cOptions = optimoptions(@fmincon, 'TolFun', 0.00000001, ...
'MaxIterations', 100000, ...
'MaxFunEvals', 50000, ...
'Display', 'iter', 'Algorithm', 'sqp', ...
'StepTolerance', 1e-13, ...
'SpecifyConstraintGradient', true, ...
'SpecifyObjectiveGradient', true, ...
'ConstraintTolerance', 1e-6, ...
'CheckGradients', false, ...
'HonorBounds', true, ...
'FiniteDifferenceType', 'forward');
% Options for optimizing the actual cost function
aOptions = optimoptions(@fmincon, 'TolFun', 0.00000001, ...
'MaxIterations', 1000, ...
'MaxFunEvals', 1000000, ...
'Display', 'iter', 'Algorithm', 'sqp', ...
'StepTolerance', 1e-13, ...
'SpecifyConstraintGradient', true, ...
'SpecifyObjectiveGradient', true, ...
'ConstraintTolerance', 1e-6, ...
'CheckGradients', false, ...
'HonorBounds', true, ...
'FiniteDifferenceType', 'forward');
% No linear inequality or equality constraints
A = [];
B = [];
Aeq = [];
Beq = [];
% Set up the bounds
[lb, ub] = bounds(sp);
tic
numVars = size(sp.phases, 1) * 2 - 1 + sp.gridn * size(sp.phases, 1) * 10;
funparams = conj(sym('x', [1 numVars], 'real')');
if GEN_CONSTRAINTS
fprintf('Generating constraints...\n');
[c, ceq] = constraints(funparams, sp);
cjac = jacobian(c, funparams).';
ceqjac = jacobian(ceq, funparams).';
constraintsFun = matlabFunction(c, ceq, cjac, ceqjac, 'Vars', {funparams});
fprintf('Done generating constraints...\n');
end
if GEN_COSTS
fprintf('Generating costs...\n');
ccost = constcost(funparams, sp);
ccostjac = jacobian(ccost, funparams).';
ccostFun = matlabFunction(ccost, ccostjac, 'Vars', {funparams});
acost = actsqrcost(funparams, sp);
acostjac = jacobian(acost, funparams).';
acostFun = matlabFunction(acost, acostjac, 'Vars', {funparams});
awcost = actworkcost(funparams, sp);
awcostjac = jacobian(awcost, funparams).';
awcostFun = matlabFunction(awcost, awcostjac, 'Vars', {funparams});
fprintf('Done generating costs...\n');
end
flag = -1;
tryCount = 0;
while flag < 0 && tryCount < 3
fprintf('Generating initial possible trajectory (%d)...\n', tryCount+1);
% Generate initial guess
x0 = MinMaxCheck(lb, ub, ones(numVars, 1) * rand() * 2);
[ci, ceqi, cjaci, ceqjaci] = constraintsFun(x0);
while any(imag(ci)) || any(imag(ceqi)) || any(any(imag(cjaci))) || any(any(imag(ceqjaci))) || ...
any(isnan(ci)) || any(isnan(ceqi)) || any(any(isnan(cjaci))) || any(any(isnan(ceqjaci))) || ...
any(isinf(ci)) || any(isinf(ceqi)) || any(any(isinf(cjaci))) || any(any(isinf(ceqjaci)))
fprintf('Regenerating initial guess...\n');
x0 = MinMaxCheck(lb, ub, ones(numVars, 1) * rand());
[ci, ceqi, cjaci, ceqjaci] = constraintsFun(x0);
end
% Find any feasible trajectory
[feasible, ~, flag, ~] = ...
fmincon(@(x) call(ccostFun, x, 2),x0,A,B,Aeq,Beq,lb,ub, ...
@(x) call(constraintsFun, x, 4), cOptions);
tryCount = tryCount + 1;
end
if flag > 0
fprintf('Optimizing for torque/raddot squared...\n');
% Optimize for torque/raddot squared cost
[optimal, ~, ~, ~] = ...
fmincon(@(x) call(acostFun, x, 2),feasible,A,B, ...
Aeq,Beq,lb,ub,@(x) call(constraintsFun,x,4),aOptions);
fprintf('Optimizing for work...\n');
% Optimize for minimum work
[optimal, cost, flag, ~] = ...
fmincon(@(x) call(awcostFun, x, 2),optimal,A,B, ...
Aeq,Beq,lb,ub,@(x) call(constraintsFun,x,4),aOptions);
fprintf('Done optimizing\n');
else
optimal = [];
cost = 0;
fprintf('Exited with non-positive flag: %d\n', flag);
end
fprintf('Finished optimizing in %f seconds\n', toc);
constraints.m
function [ c, ceq ] = constraints( funparams, sp )
% Phase inequality constraints
phaseIC = sym('pic', [1, 4*sp.gridn*size(sp.phases, 1)])';
% Phase equality constraints
phaseEC = sym('pec', [1, 8*(sp.gridn-1)*size(sp.phases, 1)])';
% Phase transition equality constraints
transEC = sym('tec', [1, 8*(size(sp.phases, 1)-1)])';
% Unpack the parameter vector
[ stanceT, flightT, xtoe, xtoedot, x, xdot, y, ydot, ...
ra, radot, raddot, torque] = unpack(funparams, sp);
% Iterate over all the phases
for p = 1 : size(sp.phases, 1)
phaseStr = sp.phases(p, :);
% The index of the first dynamics variable for the current phase
ps = (p - 1) * sp.gridn + 1;
% Calculate the timestep for that specific phase
dt = stanceT(p) / sp.gridn;
% Take off state at the end of the last phase
if p > 1
toState = stateN;
toCompvars = compvarsN;
end
stateN = [xtoe(ps); xtoedot(ps); x(ps); xdot(ps); ...
y(ps); ydot(ps); ra(ps); radot(ps)];
% Link ballistic trajectory from end of last phase to this phase
if p > 1
rland = sqrt((x(ps) - xtoe(ps))^2 + y(ps)^2);
[xtoedotland, xland, xdotland, yland, ydotland] = ...
ballistic(toState, flightT(p-1), sp, phaseStr);
% Grf must equal zero at takeoff
transEC((p-2)*8+1 : (p-1)*8) = ...
[xtoedotland-xtoedot(ps); xland-x(ps); ...
xdotland-xdot(ps); yland-y(ps); ydotland-ydot(ps); ...
ra(ps) - rland; radot(ps); toCompvars.grf];
end
% Offset in the equality parameter vector due to phase
pecOffset = 8 * (sp.gridn - 1) * (p - 1);
% Offset in the inequality parameter vector due to phase
picOffset = 4 * (sp.gridn) * (p - 1);
[statedotN, compvarsN] = dynamics(stateN, raddot(ps), ...
torque(ps), sp, phaseStr);
for i = 1 : sp.gridn - 1
% The state at the beginning of the time interval
stateI = stateN;
% What the state should be at the end of the time interval
stateN = [xtoe(ps+i); xtoedot(ps+i); x(ps+i); xdot(ps+i); ...
y(ps+i); ydot(ps+i); ra(ps+i); radot(ps+i)];
% The state derivative at the beginning of the time interval
statedotI = statedotN;
% Some calculated variables at the beginning of the interval
compvarsI = compvarsN;
% The state derivative at the end of the time interval
[statedotN, compvarsN] = ...
dynamics(stateN, raddot(ps+i), torque(ps+i), sp, phaseStr);
% The end position of the time interval calculated using quadrature
endState = stateI + dt * (statedotI + statedotN) / 2;
% Constrain the end state of the current time interval to be
% equal to the starting state of the next time interval
phaseEC(pecOffset+(i-1)*8+1:pecOffset+i*8) = stateN - endState;
% Constrain the length of the leg, grf, and body y pos
phaseIC(picOffset+(i-1)*4+1 : picOffset+i*4) = ...
[compvarsI.r - sp.maxlen; sp.minlen - compvarsI.r; ...
-compvarsI.grf; compvarsI.grf - sp.maxgrf];
end
if p == size(sp.phases, 1)
% Constrain the length of the leg at the end position
% Since it's the end of the last phase, add grf constraint
phaseIC(picOffset+(sp.gridn-1)*4+1:picOffset+sp.gridn*4) = ...
[compvarsN.r - sp.maxlen; sp.minlen - compvarsN.r; ...
-compvarsN.grf; compvarsN.grf - sp.maxgrf];
else
% Constrain the length of the leg at the end position
% No ground reaction force constraint (this will be handled in
% transition equality constraints)
phaseIC(picOffset+(sp.gridn-1)*4+1:picOffset+sp.gridn*4) = ...
[compvarsN.r - sp.maxlen; sp.minlen - compvarsN.r; -1; -1];
end
end
c = phaseIC;
ceq = [phaseEC; transEC];
initialState = [xtoe(1); xtoedot(1); x(1); xdot(1); ...
y(1); ydot(1); ra(1); radot(1)];
% Add first phase start constraints
ceq = [ceq; initialState - sp.initialState];
% Add last phase end constraints
ceq = [ceq; x(end) - sp.finalProfileX; xtoe(end) - sp.finalProfileX];
end
unpack.m
function [ stanceT, flightT, xtoe, xtoedot, x, xdot, y, ydot, ...
ra, radot, raddot, torque] = unpack( funparams, sp )
p = size(sp.phases, 1);
cnt = sp.gridn * p;
stanceT = funparams(1 : p);
flightT = funparams(p + 1 : p * 2 - 1);
xtoe = funparams(p * 2 : p * 2 - 1 + cnt);
xtoedot = funparams(p * 2 + cnt : p * 2 - 1 + cnt * 2);
x = funparams(p * 2 + cnt * 2 : p * 2 - 1 + cnt * 3);
xdot = funparams(p * 2 + cnt * 3 : p * 2 - 1 + cnt * 4);
y = funparams(p * 2 + cnt * 4 : p * 2 - 1 + cnt * 5);
ydot = funparams(p * 2 + cnt * 5 : p * 2 - 1 + cnt * 6);
ra = funparams(p * 2 + cnt * 6 : p * 2 - 1 + cnt * 7);
radot = funparams(p * 2 + cnt * 7 : p * 2 - 1 + cnt * 8);
raddot = funparams(p * 2 + cnt * 8 : p * 2 - 1 + cnt * 9);
torque = funparams(p * 2 + cnt * 9 : p * 2 - 1 + cnt * 10);
end
dynamics.m
function [ statedot, compvars ] = dynamics( state, raddot, torque, sp, curPhase )
stateCell = num2cell(state');
[xtoe, xtoedot, x, xdot, y, ydot, ra, radot] = deal(stateCell{:});
r = sqrt((x - xtoe)^2 + y^2);
rdot = ((x-xtoe)*(xdot-xtoedot)+y*ydot)/(r);
cphi = (x-xtoe) / r;
sphi = y / r;
fs = sp.spring * (ra - r) + sp.damp * (radot - rdot);
ft = torque / r;
fg = sp.masship * sp.gravity;
xddot = (1/sp.masship) * (fs*cphi + ft * sphi);
yddot = (1/sp.masship) * (fs*sphi + ft * (-cphi) - fg);
grf = fs * sphi - ft * cphi + sp.masstoe * sp.gravity;
% Check if the phase should be slipping
if strcmp(curPhase, 'sli')
ff = -sp.friction * tanh(xtoedot * 50) * grf;
xtoeddot = (1/sp.masstoe) * (-fs*cphi - ft*sphi + ff);
else
xtoeddot = 0;
end
statedot = [xtoedot; xtoeddot; xdot; xddot; ydot; yddot; ...
radot; raddot];
compvars.r = r;
compvars.grf = grf;
end
ballistic.m
function [ xtoedotland, xland, xdotland, yland, ydotland ] = ...
ballistic( toState, flightTime, sp, curPhase )
stateCell = num2cell(toState');
[~, ~, x, xdot, y, ydot, ~, ~] = deal(stateCell{:});
if strcmp(curPhase, 'sli')
xtoedotland = xdot;
else
xtoedotland = 0;
end
xland = x + xdot * flightTime;
yland = y + ydot * flightTime - 0.5 * sp.gravity * flightTime^2;
xdotland = xdot;
ydotland = ydot - sp.gravity * flightTime;
end
constcost.m
function [ cost ] = constcost( funparams, sp )
cost = sym(1);
end
actsqrcost.m
function [ cost ] = actsqrcost( funparams, sp )
% Unpack the vector
[stanceT, ~, ~, ~, ~, ~, ~, ~, ~, ~, raddot, torque] = ...
unpack(funparams, sp);
dts = kron(stanceT./sp.gridn, ones(sp.gridn, 1));
cost = sum((raddot .* dts) .^ 2) + sum((torque .* dts) .^ 2);
end
actworkcost.m
function [ cost ] = actworkcost( funparams, sp )
% Unpack the vector
[stanceT, ~, xtoe, ~, x, xdot, y, ydot, ra, radot, ~, torque] = ...
unpack(funparams, sp);
phaseN = size(sp.phases, 1);
r = sqrt((x - xtoe).^2 + y.^2);
rdot = ((x-xtoe).*(xdot)+y.*ydot)./(r);
fs = sp.spring * (ra - r) + sp.damp * (radot - rdot);
startRemInd = 1 : sp.gridn : sp.gridn * phaseN;
endRemInd = sp.gridn : sp.gridn : sp.gridn * phaseN;
[fsA, fsB] = deal(fs);
fsA(startRemInd) = [];
fsB(endRemInd) = [];
fsCombined = (fsA + fsB) .* 0.5;
[radotA, radotB] = deal(radot);
radotA(startRemInd) = [];
radotB(endRemInd) = [];
radotCombined = (radotA + radotB) .* 0.5;
epsilon = 0.001;
workRa = (sqrt((fsCombined.*radotCombined).^2 + epsilon^2) - epsilon);
workRa = workRa .* kron(stanceT./sp.gridn, ones(sp.gridn - 1, 1));
angles = atan2(y, x - xtoe);
angleShift = [angles(1); angles(1 : end-1)];
angleDeltas = angles - angleShift;
angleDeltas(startRemInd) = [];
[torqueA,torqueB] = deal(torque);
torqueA(startRemInd) = [];
torqueB(endRemInd) = [];
torqueCombined = (torqueA + torqueB) .* 0.5;
workAng = sqrt((torqueCombined.*angleDeltas).^2 + epsilon^2) - epsilon;
cost = sum(workRa) + sum(workAng);
end
bounds.m
function [ lb, ub ] = bounds(sp)
stanceTimeMin = sp.minStanceTime;
stanceTimeMax = sp.maxStanceTime;
flightTimeMin = sp.minFlightTime;
flightTimeMax = sp.maxFlightTime;
minXtoedot = -Inf;
maxXtoedot = Inf;
minX = -Inf;
maxX = Inf;
minXdot = -Inf;
maxXdot = Inf;
minY = 0;
maxY = Inf;
minYdot = -Inf;
maxYdot = Inf;
minRa = -Inf;
maxRa = Inf;
minRadot = -Inf;
maxRadot = Inf;
minRaddot = sp.minraddot;
maxRaddot = sp.maxraddot;
minTorque = sp.mintorque;
maxTorque = sp.maxtorque;
minXtoe = [];
maxXtoe = [];
for p=1:size(sp.phases, 1)
phase = sp.phases(p, :);
if strcmp(phase, 'sli')
minXtoe = [minXtoe; ones(sp.gridn, 1) * sp.slipPatch(1)];
maxXtoe = [maxXtoe; ones(sp.gridn, 1) * sp.slipPatch(2)];
elseif strcmp(phase, 'stl')
minXtoe = [minXtoe; ones(sp.gridn, 1) * -Inf];
maxXtoe = [maxXtoe; ones(sp.gridn, 1) * sp.slipPatch(1)];
elseif strcmp(phase, 'str')
minXtoe = [minXtoe; ones(sp.gridn, 1) * sp.slipPatch(2)];
maxXtoe = [maxXtoe; ones(sp.gridn, 1) * Inf];
end
end
stanceTimeVars = ones(size(sp.phases, 1), 1);
flightTimeVars = ones(size(sp.phases, 1) - 1, 1);
gridVars = ones(sp.gridn * size(sp.phases, 1), 1);
lb = [stanceTimeVars * stanceTimeMin; flightTimeVars * flightTimeMin;
minXtoe; gridVars * minXtoedot;
gridVars * minX; gridVars * minXdot;
gridVars * minY; gridVars * minYdot;
gridVars * minRa; gridVars * minRadot;
gridVars * minRaddot; gridVars * minTorque];
ub = [stanceTimeVars * stanceTimeMax; flightTimeVars * flightTimeMax;
maxXtoe; gridVars * maxXtoedot;
gridVars * maxX; gridVars * maxXdot;
gridVars * maxY; gridVars * maxYdot;
gridVars * maxRa; gridVars * maxRadot;
gridVars * maxRaddot; gridVars * maxTorque];
end
randState.m
function [ state ] = randState( slipPatch )
sp = SimParams();
% Generate random initial hip x with 0.3 meter margin from patch edges
x = rand() * (slipPatch(2) - 0.6) + 0.3;
% Random initial hip x vel must be positive
xdot = rand() * 0.5;
% Random toe x within 0.2 forward of hip x
xtoe = x + rand() * 0.2;
% Toe x vel equal to hip x vel
xtoedot = xdot;
% Y calculated assuming rtouchdown = maxlen
y = sqrt(sp.maxlen ^ 2 - (x - xtoe) ^ 2);
% Y vel some random downward number
ydot = -rand() * 0.4;
% Actuated length at max length, and initial actuated length derivative
% is zero
ra = sp.maxlen;
radot = 0;
state = [xtoe; xtoedot; x; xdot; y; ydot; ra; radot];
end
call.m
function [varargout] = call(fun, x, nout)
% Calls the specific function, specifying number of output args
varargout = cell(nout, 1);
[varargout{:}] = fun(x);
end
SimParams.m
classdef SimParams < handle
properties
% Order of phases (sli=slip, stl=stick left side of patch, str =
% stick right side of patch
phases
% The region of slippery terrain
slipPatch
% The initial state of the SLIP over the ice
initialState
% The final x position of the toe and the hip
finalProfileX
gridn = 10; % Number of grid points during stance phase
masship = 1; % Mass of body in kilograms
masstoe = 0.1; % Mass of the toe in kilograms
spring = 20; % Spring coefficient
damp = 0.5; % Damping coefficient
gravity = 1; % Gravity
% Friction coefficient between toe and ground on slippery surfaces
friction = 0.05;
minStanceTime = 0.1; % Minimum stance phase time
maxStanceTime = 2; % Maximum stance phase time
minFlightTime = 0; % Minimum flight phase time
maxFlightTime = 5; % Maximum flight phase time
minraddot = -1; % Minimum second deriv of actuated length
maxraddot = 1; % Maximum second deriv of actuated length
mintorque = -1; % Minimum torque at hip
maxtorque = 1; % Maximum torque at hip
minlen = 0.5; % Minimum length of the leg
maxlen = 1; % Maximum length of the leg
maxgrf = 10; % Maximum ground reaction force
end
methods
function obj = SimParams(phases, slipPatch, initialState, finProfX)
if nargin == 0
phases = [];
slipPatch = [];
initialState = [];
finProfX = 0;
end
obj.phases = phases;
obj.slipPatch = slipPatch;
obj.initialState = initialState;
obj.finalProfileX = finProfX;
end
function iss = iss(obj)
iss = struct();
iss.xtoe = obj.initialState(1);
iss.xtoedot = obj.initialState(2);
iss.x = obj.initialState(3);
iss.xdot = obj.initialState(4);
iss.y = obj.initialState(5);
iss.ydot = obj.initialState(6);
iss.ra = obj.initialState(7);
iss.radot = obj.initialState(8);
end
end
end
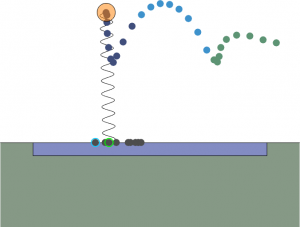
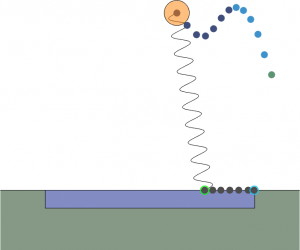
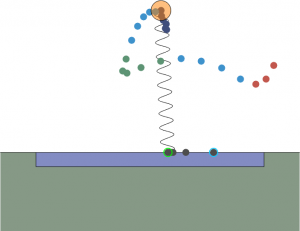
Visualization of trajectories and other stuff relevant to my research project (more on that later) is on GitHub. Include visualize.m, animate.m, VisParams.m, and rewind.gif to look at the optimized trajectories. My apologies for the slightly messy code. Here’s some images of what the trajectories look like:
Key: dark blue (slide phase), green (first stick phase), red (second stick phase), light blue (flight phase), black (toe position), green highlight (landing), blue highlight (takeoff)—dots equally time-spaced, SLIP in starting state.

Leave a Reply